Chapter 3 Basic Data Types

Exercise 3.1: If the function f returns a non-finite float64 value, the SVG file will contain invalid <polygon> elements (although many SVG renderers handle this gracefully). Modify the program to skip invalid polygons.

// func main()
//...
    ax, ay, err := corner(i+1, j)
    if err != nil {
        continue
    }
//...

func corner(i, j int) (float64, float64, error) {
    // Find point (x,y) at corner of cell (i,j).
    x := xyrange * (float64(i)/cells - 0.5)
    y := xyrange * (float64(j)/cells - 0.5)

    // Compute surface height z.
    z := f(x, y)

    // check
    if math.IsInf(z, 0) || math.IsNaN(z) {
        return 0, 0, fmt.Errorf("invalid value")
    }

    // Project (x,y,z) isometrically onto 2-D SVG canvas (sx,sy).
    sx := width/2 + (x-y)*cos30*xyscale
    sy := height/2 + (x+y)*sin30*xyscale - z*zscale
    return sx, sy, nil
}

Exercise 3.2: Experiment with visualizations of other functions from the math package. Can you produce an egg box, moguls, or a saddle?

// egg box, moguls or a saddle?
// see chapter7 7.9 for other example
// f = pow(2,sin(y))*pow(2,sin(x))/12

func f(x, y float64) float64 {
    return math.Pow(2, math.Sin(x)) * math.Pow(2, math.Sin(y)) / 12
}

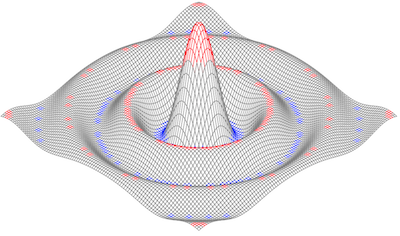
Exercise 3.3: Color each polygon based on its height, so that the peaks are colored red (#ff0000) and the valleys blue (#0000ff).

// Copyright © 2017 [email protected]
// Copyright © 2016 Alan A. A. Donovan & Brian W. Kernighan.
// License: https://creativecommons.org/licenses/by-nc-sa/4.0/

// See page 58.
//!+

// Surface computes an SVG rendering of a 3-D surface function.
package main

import (
    "fmt"
    "math"
)

const (
    width, height = 600, 320            // canvas size in pixels
    cells         = 100                 // number of grid cells
    xyrange       = 30.0                // axis ranges (-xyrange..+xyrange)
    xyscale       = width / 2 / xyrange // pixels per x or y unit
    zscale        = height * 0.4        // pixels per z unit
    angle         = math.Pi / 6         // angle of x, y axes (=30°)
)

type CornerType int

const (
    middle CornerType = 0 // not the peak or valley of surface
    peak   CornerType = 1 // the peak of surface corner
    valley CornerType = 2 // the valley of surface corner
)

var sin30, cos30 = math.Sin(angle), math.Cos(angle) // sin(30°), cos(30°)

func main() {
    fmt.Printf("<svg xmlns='http://www.w3.org/2000/svg' "+
        "style='stroke: grey; fill: white; stroke-width: 0.7' "+
        "width='%d' height='%d'>", width, height)
    for i := 0; i < cells; i++ {
        for j := 0; j < cells; j++ {
            ax, ay, ct, err := corner(i+1, j)
            if err != nil {
                continue
            }
            bx, by, ct1, err := corner(i, j)
            if err != nil {
                continue
            }
            cx, cy, ct3, err := corner(i, j+1)
            if err != nil {
                continue
            }
            dx, dy, ct2, err := corner(i+1, j+1)
            if err != nil {
                continue
            }

            var color string
            if ct == peak || ct1 == peak || ct2 == peak || ct3 == peak {
                color = "#f00"
            } else if ct == valley || ct1 == valley || ct2 == valley || ct3 == valley {
                color = "#00f"
            } else {
                // same as default
                color = "grey"
            }

            fmt.Printf("<polygon points='%g,%g %g,%g %g,%g %g,%g' style='stroke: %s'/>\n",
                ax, ay, bx, by, cx, cy, dx, dy, color)
        }
    }
    fmt.Println("</svg>")
}

func corner(i, j int) (float64, float64, CornerType, error) {
    // Find point (x,y) at corner of cell (i,j).
    x := xyrange * (float64(i)/cells - 0.5)
    y := xyrange * (float64(j)/cells - 0.5)

    // Compute surface height z.
    z, ct := f(x, y)

    // check
    if math.IsInf(z, 0) || math.IsNaN(z) {
        return 0, 0, 0, fmt.Errorf("invalid value")
    }

    // Project (x,y,z) isometrically onto 2-D SVG canvas (sx,sy).
    sx := width/2 + (x-y)*cos30*xyscale
    sy := height/2 + (x+y)*sin30*xyscale - z*zscale
    return sx, sy, ct, nil
}

func f(x, y float64) (float64, CornerType) {
    d := math.Hypot(x, y) // distance from (0,0)
    ct := middle

    // f(x) = sin(x)/x, f'(x) = (x*cos(x)-sin(x))/x^2
    // f'(x) = 0 ==> x = tan(x), peak or vally
    // if f''(x) > 0, vally
    // if f''(x) < 0, peak
    // f''(x) = {2(sin(x)-x*cos(x)) - x*x*sin(x)}/x*x*x
    if math.Abs(d-math.Tan(d)) < 3 {
        ct = peak
        if 2*(math.Sin(d)-d*math.Cos(d))-d*d*math.Sin(d) > 0 {
            ct = valley
        }
    }
    return math.Sin(d) / d, ct
}

//!-

key points:

$f(x)=\frac {sin(x)}{x}$

$f'(x) = \frac {xcos(x) - sin(x)}{x2}$

$f''(x) = \frac {2(sin(x)-xcos(x)) - x2sin(x)} {x3}$

$f'(x) = 0 \to xcos(x) = sin(x) \to x = tan(x)$

if $f'(x) = 0, f''(x) > 0$ , f(x) is peak;

if $f'(x) = 0, f''(x) < 0$ , then f(x) is valley.

Exercise 3.4: Following the approach of the Lissajous example in Section 1.7, construct a web server that computes surfaces and writes SVG data to the client. The server must set the Content-Type header like this:

w.Header().Set("Content-Type", "image/svg+xml")

(This step was not required in the Lissajous example because the server uses standard heuristics to recognize common formats like PNG from the first 512 bytes of the response and generates the proper header.) Allow the client to specify values like height, width, and color as HTTP request parameters.

// Copyright © 2017 [email protected]
// Copyright © 2016 Alan A. A. Donovan & Brian W. Kernighan.
// License: https://creativecommons.org/licenses/by-nc-sa/4.0/

// See page 58.
//!+

// Surface computes an SVG rendering of a 3-D surface function.
package main

import (
    "fmt"
    "math"
    "io"
    "net/http"
    "log"
    "strconv"
)

const (
    cells   = 100         // number of grid cells
    xyrange = 30.0        // axis ranges (-xyrange..+xyrange)
    angle   = math.Pi / 6 // angle of x, y axes (=30°)
)

var (
    width, height float64 = 600, 320
    xyscale               = width / 2 / xyrange // pixels per x or y unit
    zscale                = height * 0.4        // pixels per z unit
)

var sin30, cos30 = math.Sin(angle), math.Cos(angle) // sin(30°), cos(30°)

func main() {
    http.HandleFunc("/", func(writer http.ResponseWriter, request *http.Request) {
        // parse width/height
        if err := request.ParseForm(); err != nil {
            log.Printf("parseForm: %v\n", err)
        }
        for k, v := range request.Form {
            var err error

            if k == "width" {
                if width, err = strconv.ParseFloat(v[0], 64); err != nil {
                    width = 600
                    log.Printf("parseWidth: %v\n", err)
                }
            }

            if k == "height" {
                if height, err = strconv.ParseFloat(v[0], 64); err != nil {
                    height = 320
                    log.Printf("parseHeight: %v\n", err)
                }
            }
        }

        // need recalculate
        xyscale = width / 2 / xyrange // pixels per x or y unit
        zscale = height * 0.4         // pixels per z unit

        writer.Header().Set("Content-Type", "image/svg+xml")
        surface(writer)
    })
    log.Fatal(http.ListenAndServe("localhost:8000", nil))
}

func surface(w io.Writer) {
    fmt.Fprintf(w, "<svg xmlns='http://www.w3.org/2000/svg' "+
        "style='stroke: grey; fill: white; stroke-width: 0.7' "+
        "width='%d' height='%d'>", int64(width), int64(height))
    for i := 0; i < cells; i++ {
        for j := 0; j < cells; j++ {
            ax, ay := corner(i+1, j)
            bx, by := corner(i, j)
            cx, cy := corner(i, j+1)
            dx, dy := corner(i+1, j+1)
            fmt.Fprintf(w, "<polygon points='%g,%g %g,%g %g,%g %g,%g'/>\n",
                ax, ay, bx, by, cx, cy, dx, dy)
        }
    }
    fmt.Fprintln(w, "</svg>")
}

//!-

Exercise 3.5: Implement a full-color Mandelbrot set using the function image.NewRGBA and the type color.RGBA or color.YCbCr.

// 16 colors, for same escape time
var palettes = [...]color.RGBA{
    {66, 30, 15, 255},
    {25, 7, 26, 255},
    {9, 1, 47, 255},
    {4, 4, 73, 255},
    {0, 7, 100, 255},
    {12, 44, 138, 255},
    {24, 82, 177, 255},
    {57, 125, 209, 255},
    {134, 181, 229, 255},
    {211, 236, 248, 255},
    {241, 233, 191, 255},
    {248, 201, 95, 255},
    {255, 170, 0, 255},
    {204, 128, 0, 255},
    {153, 87, 0, 255},
    {106, 52, 3, 255},
}

func mandelbrot(z complex128) color.Color {
    const iterations = 255
    const contrast = 15

    var v complex128
    for n := uint8(0); n < iterations; n++ {
        v = v*v + z
        if cmplx.Abs(v) > 2 {
            return palettes[n%16]
        }
    }
    return color.Black
}

colors from here, basically same escape time should have same color.

Exercise 3.6: Supersampling is a technique to reduce the effect of pixelation by computing the color value at several points within each pixel and taking the average. The simplest method is to divide each pixel into four ‘‘subpixels.’’ Implement it.

// skip for now

Exercise 3.7: Another simple fractal uses Newton’s method to find complex solutions to a function such as $z4−1 = 0$ . Shade each starting point by the number of iterations required to get close to one of the four roots. Color each point by the root it approaches.

// from book author
// f(x) = x^4 - 1
//
// z' = z - f(z)/f'(z)
//    = z - (z^4 - 1) / (4 * z^3)
//    = z - (z - 1/z^3) / 4
func newton(z complex128) color.Color {
    const iterations = 37
    const contrast = 7
    for i := uint8(0); i < iterations; i++ {
        z -= (z - 1/(z*z*z)) / 4
        if cmplx.Abs(z*z*z*z-1) < 1e-6 {
            return color.Gray{255 - contrast*i}
        }
    }
    return color.Black
}

Exercise 3.8: Rendering fractals at high zoom levels demands great arithmetic precision. Implement the same fractal using four different representations of numbers: complex64, complex128, big.Float, and big.Rat. (The latter two types are found in the math/big package. Float uses arbitrary but bounded-precision floating-point; Rat uses unbounded-precision rational numbers.) How do they compare in performance and memory usage? At what zoom levels do rendering artifacts become visible?

// skip for now: how to control zoom level?

Exercise 3.9: Write a web server that renders fractals and writes the image data to the client. Allow the client to specify thex,y, and zoom values as parameters to the HTTP request.

// skip for now: how to control zoom level?

Exercise 3.10: Write a non-recursive version of comma, using bytes.Buffer instead of string concatenation.

// comma inserts commas in a non-negative decimal integer string.
func comma(s string) string {
    n := len(s)
    if n <= 3 {
        return s
    }

    var buf bytes.Buffer
    d, t := len(s)%3, len(s)/3

    if d != 0 {
        buf.WriteString(s[:d])
        buf.WriteByte(',')
    }

    for i := 0; i < t; i++ {
        buf.WriteString(s[i*3+d:d+i*3+3])
        if i != t-1 {
            buf.WriteByte(',')
        }
    }
    return buf.String()
}

Exercise 3.11: Enhance comma so that it deals correctly with floating-point numbers and an optional sign.

// comma inserts commas in a non-negative decimal integer string.
func comma(s string) string {
    var sign string

    // skip optional sign flag
    if hasSign := strings.HasPrefix(s, "+") ||
        strings.HasPrefix(s, "-"); hasSign {
        sign = s[0:1]
        s = s[1:]
    }

    var buf bytes.Buffer
    buf.WriteString(sign)

    if period := strings.LastIndex(s, "."); period != -1 {
        doWork(s[:period], &buf)
        buf.WriteByte('.')
        doWork(s[period+1:], &buf)
    } else {
        doWork(s, &buf)
    }

    return buf.String()
}

// add to only one buf
func doWork(s string, buf *bytes.Buffer) {
    n := len(s)
    if n <= 3 {
        buf.WriteString(s)
        return
    }

    d, t := len(s)%3, len(s)/3
    if d != 0 {
        buf.WriteString(s[:d])
        buf.WriteByte(',')
    }

    for i := 0; i < t; i++ {
        buf.WriteString(s[i*3+d:d+i*3+3])
        if i != t-1 {
            buf.WriteByte(',')
        }
    }
}

Exercise 3.12: Write a function that reports whether two strings are anagrams of each other, that is, they contain the same letters in a different order.

// first construct a map with s1, then check s2 with map
// map is rune:int pair
func anagram(s1, s2 string) bool {
    m := make(map[rune]int)
    for _, r := range s1 {
        m[r]++
    }
    for _, r := range s2 {
        if i, ok := m[r]; ok {
            if i > 1 {
                m[r]--
            } else {
                delete(m, r)
            }
        } else {
            return false
        }
    }
    return len(m) == 0
}

Exercise 3.13: Write const declarations for KB, MB, up through YB as compactly as you can.

const (
    KB = 1000
    MB = 1000 * KB
    GB = 1000 * MB
    TB = 1000 * GB
    PB = 1000 * TB
    EB = 1000 * PB
    ZB = 1000 * EB
    YB = 1000 * ZB
)

Notes

Types: Go’s types fall into four categories: basic types, aggregate types, reference types, and interface types.

Basic Types	number, boolean, string
Aggregate Types	array, struct
Reference Types	pointer, slice, map, function, chan
Interface Types	interface

int/uint: There are also two types called just int and uint that are the natural or most efficient size for signed and unsigned integers on a particular platform
rune/byte: The type rune is an synonym for int32 and conventionally indicates that a value is a Unicode code point. The two names may be used interchangeably. Similarly, the type byte is an synonym for uint8, and emphasizes that the value is a piece of raw data rather than a small numeric quantity.
uintptr: There is an unsigned integer type uintptr, whose width is not specified but is sufficient to hold all the bits of a pointer value. The uintptr type is used only for low-level programming, such as at the boundary of a Go program with a C library or an operating system.
Regardless of their size, int, uint, and uintptr are different types from their explicitly sized siblings.
Binary Operator:

| * / % << >> & &^(bit clear, AND NOT) | a &^ b == a & (^b), bit clear operator | | :--- | :--- | | + - | ^ (bitwise xor, unary bitwise not/negation) | unary ^ is bitwise operator not, opposite bits 0->1, 1->0 | | == != < <= > >= | and ^b + b == -1, | | && | five level precedence , in order of decreasing | | || | associative to left in same precedence level |
%: The behavior of % for negative numbers varies across programming languages. In Go, the sign of the remainder is always the same as the sign of the dividend, so -5%3 and -5%-3 are both -2.
unsigned numbers: Tend to be used only when their bitwise operators or peculiar arithmetic operators are required, as when implementing bit sets, parsing binary file, formats, or for hashing and cryptography. They are typically not used for merely non-negative quantities.

Consider the following for loop:

for i := len(medals) - 1; i >= 0; i-- {}

if len(medias) return unsigned int, then i>=0 will always true, 
which will panic or access out of bound, so function len() will 
return int!

Rune literals are written as a character within single quotes.
float64/float32: the positive and negative infinities, which represent numbers of excessive magnitude and the result of division by zero; and NaN (‘‘not a number’’), the result of such mathematically dubious operations as 0/0 or Sqrt(-1).

var z float64

fmt.Println(z, -z, 1/z, -1/z, z/z) //  "0 -0 +Inf -Inf NaN"

// not a number can only be tested with math.IsNaN()
nan := math.NaN()

fmt.Println(nan == nan, nan < nan, nan > nan) // "false false false"

mnemonic: && is boolean multiplication, || is boolean addition.
There is no implicit conversion from a boolean value to a numeric value like 0 or 1, or vice versa.

// btoi
func btoi(b bool) int{
    if b {
        return 1
    }
    return 0
}

// itob
i != 0
or
func itob(i int) bool { return i != 0 }

string: A string is an immutable sequence of bytes.
text: Text strings are conventionally interpreted as UTF-8-encoded sequences of Unicode code points (runes). The i-th byte of a string is not necessarily the i-th character of a string, because the UTF-8 encoding of a non-ASCII code point requires two or more bytes.
string copy: Immutability means that it is safe for two copies of a string to share the same underlying memory, making it cheap to copy strings of any length.
Araw string literalis written `...`, using backquotes instead of double quotes. Within a raw string literal, no escape sequences are processed; the contents are taken literally, including backslashes and newlines, so a raw string literal may spread over several lines in the program source. The only processing is that carriage returns are deleted so that the value of the string is the same on all platforms, including those that conventionally put carriage returns in text files.
Raw string literals are a convenient way to write regular expressions, which tend to have lots of backslashes. They are also useful for HTML templates, JSON literals, command usage messages, and the like, which often extend over multiple lines.
UTF-8 is a variable-length encoding of Unicode code points as bytes. The high-order bits of the first byte of the encoding for a rune indicate how many bytes follow. It’s also a prefix code, so it can be decoded from left to right without any ambiguity or lookahead.
Go’s range loop, when applied to a string, performs UTF-8 decoding implicitly.
strings are immutable, building up strings incrementally can involve a lot of allocation and copying.
A string contains an array of bytes that, once created, is immutable. By contrast, the elements of a byte slice can be freely modified.

Strings can be converted to byte slices and back again:
s := "abc"
b := []byte(s)
s2 := string(b)

but b/s2 both need acclocate memory.

Conceptually, the []byte(s) conversion allocates a new byte array holding a copy of the bytes of s, and yields a slice that references the entirety of that array. An optimizing compiler may be able to avoid the allocation and copying in some cases, but in general copying is required to ensure that the bytes of s remain unchanged even if those of b are subsequently modified. The conversion from byte slice back to string with string(b) also makes a copy, to ensure immutability of the resulting strings2.
Constants are expressions whose value is known to the compiler and whose evaluation is guaranteed to occur at compile time, not at run time. The underlying type of every constant is a basic type: boolean, string, or number.
Many computations on constants can be completely evaluated at compile time, reducing the work necessary at run time and enabling other compiler optimizations. Errors ordinarily detected at run time can be reported at compile time when their operands are constants, such as integer division by zero, string indexing out of bounds, and any floating-point operation that would result in a non-finite value.
Untyped Constant: Constants in Go are a bit unusual. Although a constant can have any of the basic data types like int or float64, including named basic types like time.Duration, many constants are not committed to a particular type. The compiler represents these uncommitted constants with much greater numeric precision than values of basic types, and arithmetic on them is more precise than machine arithmetic; you may assume at least 256 bits of precision. There are six flavors of these uncommitted constants, called untyped boolean, untyped integer, untyped rune, untyped floating-point, untyped complex, and untyped string.

By deferring this commitment, untyped constants not only retain their higher precision until later, but they can participate in many more expressions than committed constants without requiring conversions.

Chapter 3 Basic Data Types

Chapter 3 Basic Data Types

Notes

results matching ""

No results matching ""